04 Dec 8th Grade Math Tutor – NYC Top Tutors
Cornerstone Protection
836 Euclid Avenue Suite 16, Lexington
-
Amazing assistance provided by Shannon today on my security system. I’m so grateful for your prompt, efficient, professional, and courteous service. Put me down as a customer for life!
-
One of the most painless experiences I've had. They came on time and was over the moon professional with still keeping a level of personability to it. The gentleman also went out of his way to say that my husband and Mines business … More was appreciated. Which is actually rare to be appreciated by such a great company. So thank you and we look forward to continuing services with this company.
-
I am so happy we decided to go with cornerstone. They were quick and efficient. Shannon and the installer we very friendly. We got a lot of equipment and it was still within our budget. 10/10 would definitely recommend! Thank you
-
Love the customer service and Shanon and his team go above and beyond for my restaurant. Couldn't of asked for a better security system and level of service that his team provides.
-
I have been using Cornerstone Protection service for over 5 years and I'm really happy with the service and state-of-the-art equipments and it's futures are so much in advance and friendly, I highly recommend Cornerstone Protection … More Service any and all business that need a security protection days and nights specially after business hours(Cornerstone Protection is perfect solution for your business). Owner of Cornerstone Protection is proactive with their customers and their equipments. Good experienced with Cornerstone Protection!!!
Kanu Patel -
We had a very positive experience with Alissa as a tutor for our pod of 5th grade boys from January - June 2020. She cared a lot about the boys and worked hard to create meaningful activities for them. The pod experience was invaluable … More for all of our families during a difficult year and we were so grateful to have found this partnership! We also want to appreciate Craig for helping to match us with a tutor on very short notice after we had cycled through a few folks who were not able to see the commitment through. Thanks for sticking with us!
-
Dusty was the exact person we needed to help our child finish out the school year. So grateful to him for the way he steadily encouraged her and helped her stay on track and organized. He is flexible, responsive to our needs/schedule as … More a family, and a delight to be with. We are also thankful that Craig at Themba Tutors really "gets it" and partnered us with such a wonderful tutor who was a great fit for our girl.
-
My child worked with Gillian D virtually for math enrichment. She is an excellent teacher. She took time to understand my child's specific learning style and provided tools that would be engaging. She was kind and empathetic- really … More made it her goal to connect with my child and build trust and rapport. My child started the school year with confidence and without the typically "brain-drain" that occurs over the summer, thanks to Gillian.
-
I am going into my second year as a Themba tutor. I have met so many great individuals while working for this company. Craig and the rest of the Themba team do such an excellent job picking and choosing Themba tutors that suit each client's … More individual needs! I look forward to meeting new tutors and clients in the 2021-2022 school year!
-
Our son started in a new high school, 100% remote, and was really struggling with Latin and Physics. I found Themba Tudors online and had an initial call with Craig, who was very knowledgeable, responsive, and found 2 amazing tutors for … More us. Both the Latin and the physics tutors were fantastic, connected with my son really well and helped him go from 'failing' grade to 'honors'! I will for sure continue using (and recommending!) Themba Tutors. Thank you, C, K, and W!
-
Brian is a fantastic executive functioning coach. Super helpful, flexible with hours, and tailored the experience to our needs.
-
Giulia Mercuri is a great Italian tutor! She was very responsive and accessible. Giulia put a ton of effort into preparing for each session and really helped our son with test preparation and projects. We are grateful that she was able … More to help, especially since our son did not receive any live teaching during COVID. We are happy that she was referred to us! -
As an adult student diagnosed with a learning disability during grad school, I knew I needed help dealing with my Master's program's demanding workload. I was seriously considering dropping out when I was referred to Themba Tutors. … More I was paired up with a wonderful tutor, Julie, who was a total lifesaver. I learned many techniques that I can utilize in the future as I embark on the next phase of my career.
I can wholeheartedly say after working with Themba for two years that I would not have finished my program without this organization. And I am so thankful I selected them. -
We were introduced to a wonderful tutor: Mcedwyn. He and our son, a freshman in college, worked well together. As a result, our son’s grades significantly improved. The tutor taught our son subject content and various methods to effectively … More study for quizzes and exams. Our son was also taught time management and organization. My son’s experience with the tutor made the first year of college a less intimidating experience. -
We have been with our tutor, Cailin Schiller, for two years, from 5th - 7th grade. She started as an executive functioning tutor with my daughter. From the start, she demonstrated a depth of expertise and a selective use of techniques skillfully … More adapted to my daughter’s ADHD and Math disability. Cailin made Math accessible and understandable to her in a way that even her teachers had not been able to do. She differentiated reading, writing and math tasks and assignments to tailor them to my daughter’s unique learning differences. Not only did it have an effect on her grades and her work efficiency, but she finally could do her work with less anxiety. Even my daughter’s teachers used Cailin’s guidance to modify their work with her. But most importantly, she became my daughter’s favorite resource. I can’t say how invaluable Cailin has been to my daughter’s progress and well-being. I’d recommend her a million times over. She is a gem. -
Victoria is a superb tutor. She helped my high school age daughter with her writing. Victoria's skills as a tutor, as well as her sense of humor and her engaging personality went a long way with my daughter. -
Themba Tutors provided a leaning specialist that was a perfect fit for my daughter. I told them what we were looking for and they delivered. Our tutor is responsive and flexible and makes it easy for my daughter to reach out to her own … More her own, which gives her an added sense of responsibility over her learning. As a therapist myself, I now regularly recommend Themba to my patients. A much needed and well provided service to the community!! -
The tutors at Themba are fantastic! Caitlyn McNeill helped our son academically, but also with getting organized in every subject, which he so desperately needed. She offered great advice and useful strategies that helped our son become … More a more successful student. We are using Themba tutors again this year for our daughter. We're so happy to have been referred to them! -
I'm so glad we were referred to Themba Tutors. After a great initial conversation to learn our needs, we were connected with an excellent tutor, Felicia, who is helping our high school daughter learn better organizational and executive … More skills. Highly recommended. -
We had a wonderful experience with our tutor Micaela. She helped our son not only academically but at every level. We will be forever grateful to have her in our lives. -
The tutors at Themba are fantastic! Caitlyn McNeill helped our son academically, but also with getting organized in every subject, which he so desperately needed. She offered great advice and useful strategies that helped our son become … More a more successful student. We are using Themba tutors again this year for our daughter. We're so happy to have been referred to them!
-
Paul Smith at Themba has been an exceptional tutor for my son, both in terms of teaching the subject matter and teaching how best to approach the process of learning math and executing assignments. We feel very fortunate to be working with … More Paul. -
We were very lucky to have found Edwouine Swift, my son's therapist through Themba Tutors. Thomas is 12 years old, and it is extremely difficult to get him to write. Edwouine just works her magic with him, he adores her and is so … More eager to follow her guidance. I have no doubt she will be a positive driving force in his academic future.
8TH GRADE MATH TUTOR- NYC TOP TUTORS
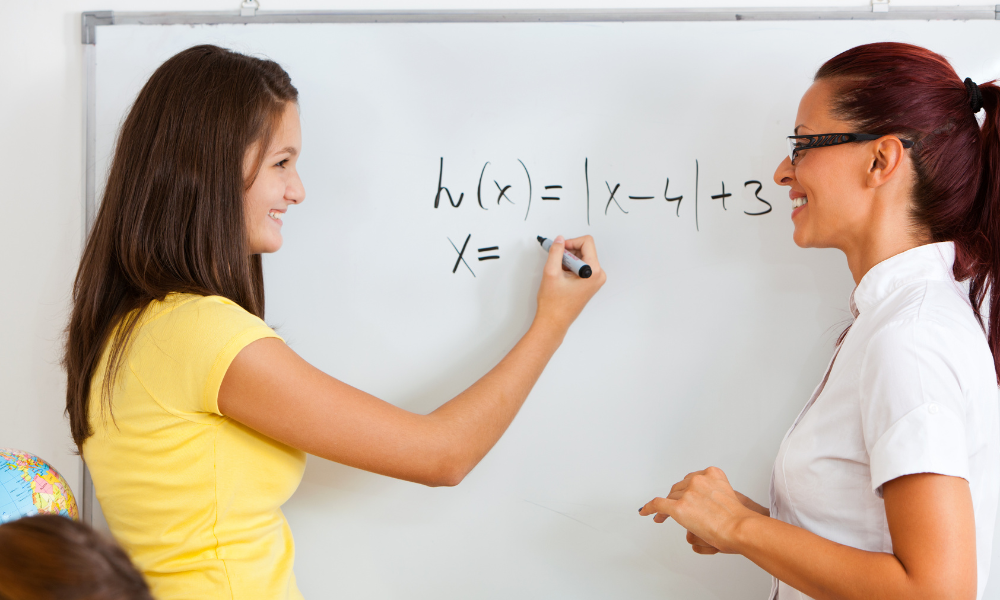
WE travel to YOUR home:
We also travel to:
8th-Grade Math Tutoring
So what exactly do students learn in 8th-grade math? We broke down 8th-grade math into the following problems and topics, like breaking down a language into parts.
If you need checklists for a breakdown of 8th grade math, we highly recommend Khan Academy and IXL for Common Core Eighth-Grade Math Standards eighth-grade standards . We also thank Embarc for breaking down 8th grade math into the following standards:
Module 1: Integer Exponents and Scientific Notation
Topic A: Exponential Notation and Properties of Integer Exponents (8.EE.A.1)
Lessons 1-6 Video Lectures:
https://www.youtube.com/watch?v=u0P7eGsvC80
https://www.youtube.com/watch?v=39iP0NjYVco
https://www.youtube.com/watch?v=yXdZuZuH5Xo
https://www.youtube.com/watch?v=_ID7r7MYXcU
https://www.youtube.com/watch?v=3zhChSM4Q7o
https://www.youtube.com/watch?v=W073q_nQLPw
Integer Exponents
In this module, students build upon the work done with exponents in the 5th, 6th, and 7th grades. They will learn the precise definition of exponential notation and how to use this definition to prove the properties of exponents.
6 x 6 means 6 (2) which is read as “6 squared”
2 x 2 x 2 means 2 (3) which is read as “2 cubed”
It is important to use parentheses when writing numbers with a negative or fractional base in.
This means that you have 2 times itself (3+4) times, then you can see that
2(3) x 2(4) = (2 x 2 x 2)(2 x 2 x 2 x 2). Using this thinking allows us to build a more abstract equation that works for any base x with positive integers m and n.
Note in these equations; the bases are the same. The next logical question is, “What if the bases aren’t the same?”
A Law of Exponents: Division
Students extend the one property of exponents defined thus far and the definition of exponents to discover a useful consequence. This consequently leads to the Law of Exponents for dividing different powers of a number.
This leads us to the more abstract conclusion that holds true for any base x and integers m and n. (Take note of the like bases.)
When first introduced, we restrict the values of m and n so that m > n until students have a conceptual understanding of negative exponents later in this module topic.
A Law of Exponents: Powers of a Power
As we progress through the module, each additional property of exponents is developed using the definition of exponents along with the previously developed properties.
Like all the others, we can then generalize this for any base x for integers m and n because
(xm)n = xm n
This law applies to products of powers raised to powers also.
ALERT: Misconception
While this last property seems simple enough, it often is misused. This law works for products, NOT sums or differences.
“The Zero-th Power”
Using various methods, students derive the definition that for any base x, x0= 1. One of the methods uses the property for dividing powers with like bases.
Negative Exponents
Negative exponents are also defined using the previous laws and previous knowledge of reciprocals 35 x 3-5 = 30
Since any base raised to the zeroth power equals 1, then 30 = 1.
Let’s take a closer look since we know 35 x 3-5 = 1 .
If multiplying 35 by the number 3-5 has a product of 1 and by definition multiplying a number by its reciprocal has a product of 1, then the number 3-5 must be mathematically equal to the reciprocal of 35. This reciprocal is 1/ 35. This idea leads to a formal definition.
For any positive number ݔ and for any positive integer ݊, we define
Once negative exponents are defined, we can perform operations using this definition and following all of the previous laws.
Example Problems and Answers:
Throughout this module, the emphasis is on understanding the laws of exponents, so encourage your student to write out all steps.
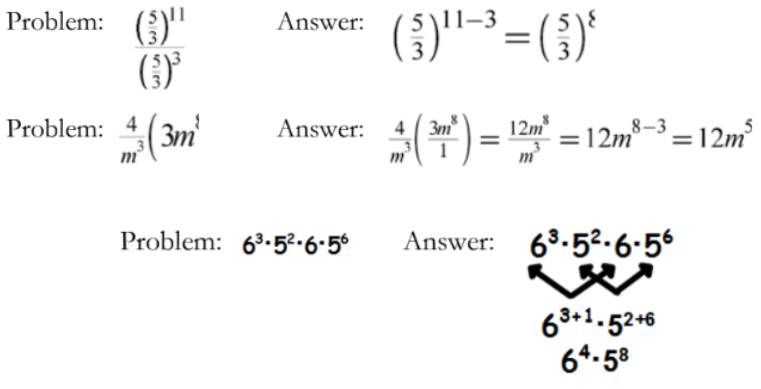
Words to Know:
Whole number – the numbers 0,1,2,3,4,5,… on the number line
Integer – the numbers …,-3,-2,-1,0,1,2,3,… on the number line
Base – the number being raised to a power (or exponent)
Exponent – the number of times a number is to be used as a factor in a multiplication expression
Power– another name for exponent
Squaring a number– multiplying a number by itself; raising a number to the second power
Cubing a number– multiplying a number by itself 3 times; raising a number to the third power
Exponential notation– a method that allows the representation of numbers in shorter form that aids in mathematical calculations.
(Example: 8 = 2 x 2 x 2 x = 23 So, 23 is considered exponential notation. The base of the exponential notation is 2, and the exponent (or power) is 3.
Reciprocal– a multiplicative inverse; the reciprocal of a number is the result when you divide a 1 by that number
(example: 12 is the reciprocal of 2 because 1 2 = 12)
Expanded form of a decimal– shows how much each digit is worth and that the number is the total of those values added together (Example: 432.56 written in the expanded form is
(4 x 102) + (3 x 101) + (2 x 100) + (5 x 10-1) + (6 x 10-2)
Topic B: Magnitude and Scientific Notation (8.EE.A.3, 8.EE.A.4)
Lessons 7-13 Video Lectures:
https://www.youtube.com/watchv=8WAGKZKP6c0
https://www.youtube.com/watchv=cD1RWdsFoBQ
https://www.youtube.com/watchv=VoT1dSYIBEQ
https://www.youtube.com/watchv=i4TULA1LVMo
https://www.youtube.com/watchv=4hUxWQ4hZVs
https://www.youtube.com/watchv=Ex6AzeV1PJw
https://www.youtube.com/watch?v=fuLKyQxZR6w
Magnitude and Scientific Notation
Example: John said that 0.009 is bigger than 0.01. Use powers of 10 to show that he is wrong.
Answer: 0.009 can be written as 9 / 1000 = 9 /10 ^3 = 9 * 10 ^ -3, and 0.01 can be written as 1 / 100 = 1 / 10^-2 = 1 * 10 ^ -2
Since 0.009 has a smaller power of ten, 0.009 is closer to zeroand smaller than 0.01.
Problem: The average American household spends $4,000 per year on gasoline. If there are 1 x 108 households, what is the total amount of money spent on gasoline by American households in one year?
Answer: $400 billion or 4 x 1011
Writing Numbers in Scientific Notation
There are a few basic characteristics of numbers written in scientific notation.
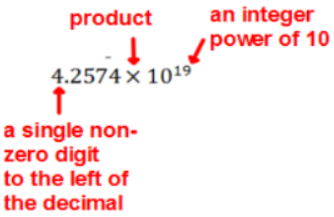
- It is a product of a decimal number (or whole number) and an integer power of 10.
- The decimal number (or whole number) must be between 1 and 10. It can be 1, but it cannot be 10 since there should only be one non-zero digit left of the decimal.
Example: 42,574,000,000,000,000,000 can be written as 4.2574 x 1019 which is in scientific notation.
Example: One hydrogen atom is approximately
0.0000000000000000000000000017 kilograms. In scientific notation, this number is 1.7 x 10-27
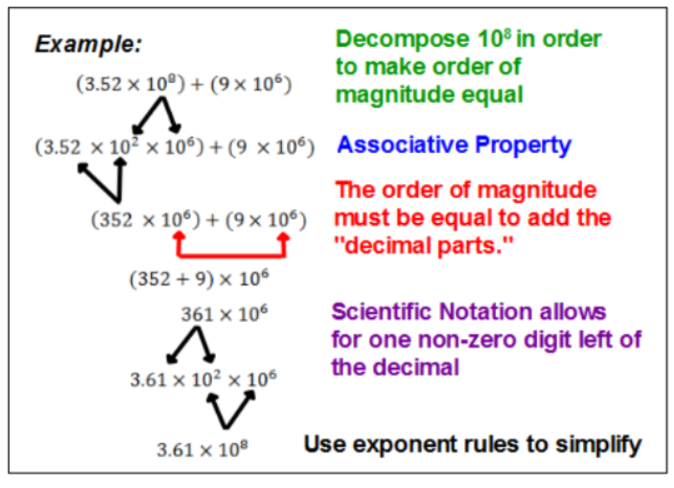
Adding or Subtracting Numbers in Scientific Notation
In order to add or subtract numbers written in scientific notation, the order of magnitude of the numbers must be equal. Just like with adding “like terms” or adding fractions, we must be adding things that are “alike” or the same size.
Subtraction follows the same guidelines only you will be subtracting the “decimal parts” of the numbers.
————————————————————————————————————————
Why do we use Scientific Notation?
- To express very small or very large numbers
- Standardizing the notation allows us to get a sense of numbers’ order of magnitude when comparing them.
- To sensibly and efficiently record and convey the results of measurements
————————————————————————————————————————
Multiplying Numbers in Scientific Notation
Since Associative and Commutative Properties hold for multiplication, we can reorder and associate the “decimal parts” and the powers of 10.
Dividing Numbers in Scientific Notation
Choice of Units
Since scientific notation is used to convey measurements, there are occasions when an arbitrary new unit can be defined out of convenience in order to compare measurements. A single lesson on this topic is devoted to creating a choice of units. A couple of examples include gigaelectronvolt as a unit of mass and light-year as a unit of distance. Students are asked to define their own units given a set of measurements. Rest assured that there are many correct “choices.” Once a unit has been chosen and clearly defined, the calculations are dependent on that new unit, and there will only be one correct calculation for measurement conversion.
Interpreting Scientific Notation Using Technology
Sometimes operations with very large or very small numbers cannot be completed with precision on a calculator, so we can convert these numbers as a sum which may be written in scientific notation or a product using powers of 10. By using distributive, commutative, and associative properties, we can then simplify to complete the calculations.
Words to Know:
Scientific Notation – the representation of a number as the product of a decimal (or whole number) and a power of 10, where the decimal number (or whole number), d, satisfies the property that it is at least 1, but smaller than 10, or in symbolic notation, 1≤ d <10. For example, the scientific notation for 192.7 is 1.927 x 102.
Order of Magnitude – the exponent in the power of 10 when that number is expressed in scientific notation. For example, the order of magnitude of 192.7 is 2 because when 192.7 is expressed in scientific notation as 1.1.927 x 102, 2 is the exponent of 102. Sometimes we also include the number 10 in the definitions of the order of magnitude and say that the order of magnitude of 192.7 is 1.927 x 102.
MEET OUR NYC TOP TUTORS WHO COULD COME TO YOUR HOME
BLAKE
High School Mathematics Teacher Completing Master’s Thesis and transitioning into his Doctoral Research at Teachers College, Columbia University
MELISSA
Certified Math and Special Education Teacher, MS Math Education
JOHN V.
Master’s in STEM Education and Master’s in Applied Math
LEAH
Bachelor’s degree in Secondary Education with a Concentration in Mathematics, M.S. in General and Special Education (grades 1-6)
DAVID
Master of Philosophy and Doctor of Philosophy, Master of Educational Leadership
DANIEL
Master’s in Elementary Education, Bachelor’s in Political Science & French
EVAN
Master’s in Leadership in Math Education, Bachelor’s Degree in Mathematics
BASSEM
M.A degree in Clinical Psychology
LEARN MORE ABOUT MATH TUTORING SERVICES:
⏩ Long Island Math Tutoring
⏩ Upper East Side Math Tutoring
⏩ North and Central NJ Math Tutoring
⏩ Long Island Middle and High School Math Tutoring
⏩ Hudson, County NJ Middle and High School Math Tutoring
⏩ Manhattan Middle and High School Math Tutoring
⏩ Bronx Middle and High School Math Tutoring
⏩Manhattan In-home Math Tutoring
⏩ Best Brooklyn Math Tutors
⏩ Remote IB Math Tutoring
Chat with Themba Tutors Today! Our 8th Grade Math Tutors are ready to help you right now!
FREE CONSULTATION WITH A NYC TUTOR!!!
Call: (917) 382-8641, Text: (833) 565-2370
Email: info@thembatutors.com
(we respond to email right away!).
Craig Selinger
Latest posts by Craig Selinger (see all)
- Unlock Your Pre-Algebra Potential with a Manhattan Pre-Algebra Tutor - February 2, 2023
- Finding the Right Brooklyn Precalculus Tutor for Your Child’s Needs - January 31, 2023
- Habits vs. Routines for College Students and their Parents - January 31, 2023
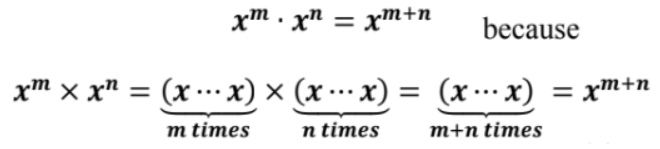
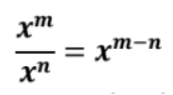
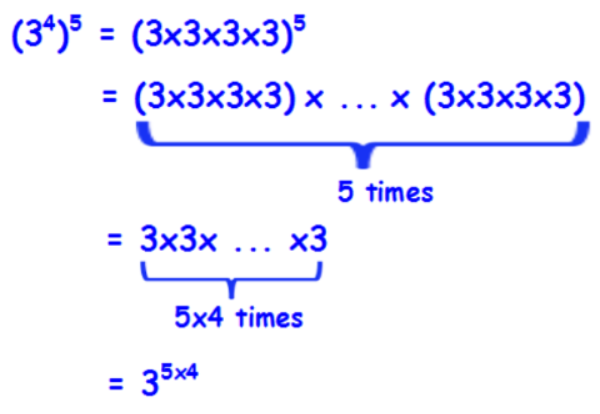
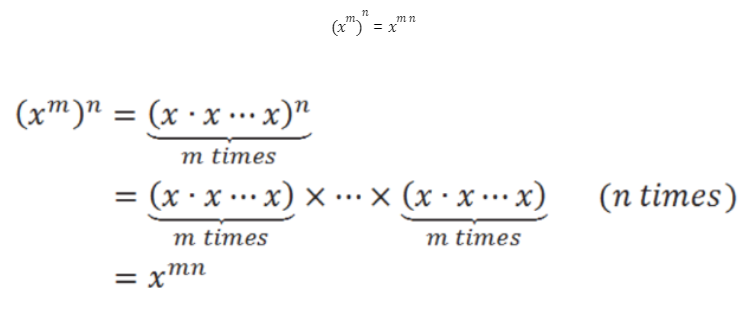
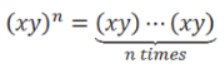
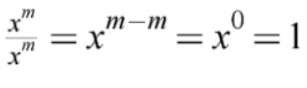
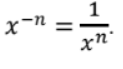
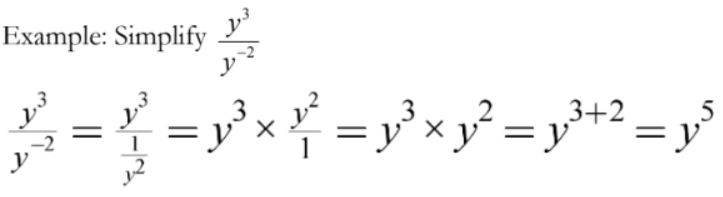
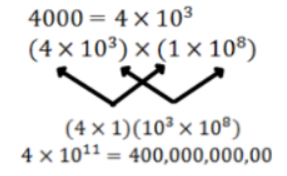
No Comments