
30 Nov 7th Grade Math Tutor – NYC Top Tutors
7TH GRADE MATH TUTOR- NYC TOP TUTORS

WE travel to YOUR home:
We also travel to:
7th-Grade Math Tutoring
So what exactly do students learn in 7th-grade math? We broke down 7th-grade math into the following problems and topics, like breaking down a language into parts.
If you need checklists for a breakdown of 7th grade math, we highly recommend Khan Academy and IXL for Common Core Seventh-Grade Math Standards. We also thank Embarc for breaking down 7th grade math into the following standards:
Module 1: Ratios and Proportional Relationships
Topic A: Proportional Relationships (7.RP.A.2a)
Lessons 1-6 Video Lectures:
https://www.youtube.com/watch?v=ycd_SxVtgtE
https://youtu.be/HUCKOf0qzeA
https://youtu.be/3Cn1MvGHIMo
https://youtu.be/3OWd3L8GNWc
https://www.youtube.com/watch?v=3FKXQHdutNQ
https://www.youtube.com/watch?v=98nqX2_QtYs
Computing Unit Rate
A 7th grade math tutor reintroduces students to the meanings of the value of a ratio, equivalent ratios, rate, and unit rate through a collaborative work task where they record their rates, choosing an appropriate unit of rate measurement.
Example Problem and Answer
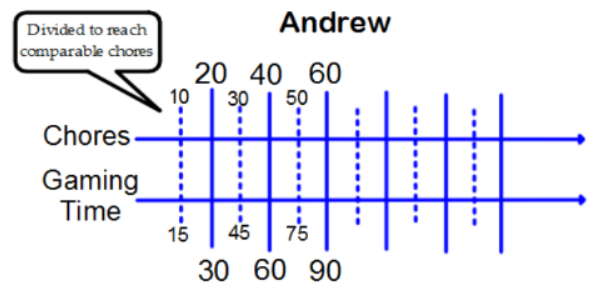
Andrew’s parents allow him 30 minutes of gaming time for every 20 chores he completes. Michael, Andrew’s older brother, receives 1 hour of gaming for every 50 chores he completes. If both boys complete the same amount of chores, do the boys get the same amount of gaming time?
Does one get more gaming time? If so, which boy gets more gaming time? Calculate the unit rate. Some students may begin by creating a double number line to represent equivalent ratios of chores to gaming time of Andrew’s chores to gaming time:
From this double number line, if both boys complete 50 chores, Andrew would receive 75 minutes of gaming and Michael 60 minutes of gaming.
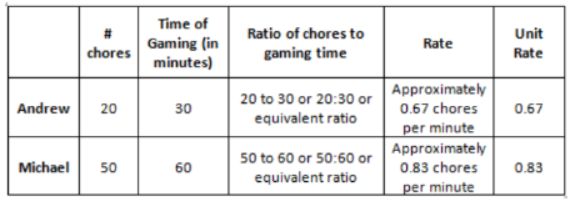
Below is a table utilized to compute the unit rate.
Also, from the table, students can notice that the unit rate is different for both boys.
Students conceptualize that two quantities are proportional to each other when a constant exists such that each measure in the first quantity multiplied by this constant gives the corresponding measure in the second quantity.
Example Problem and Answer
Jelly Beans can be purchased by ounce at Bridget’s Candy Shop. John has a family of five. The table below represents the weight of jelly beans purchased by John’s family and the total cost.
Question:
Does everyone pay the same cost per ounce? How do you know?
Solution:
Divide each cost value by its corresponding weight.
$7.20 ÷ 12 = $0.60
$8.70 ÷ 14.5 = $0.60
$4.80 ÷ 8 = $0.60
$6.00 ÷ 10 = $0.60
$12.00 ÷ 20 = $0.60
Yes, it costs $0.60 per ounce. Since we want to compare cost per ounce, we can use the unit rate to determine that we want to divide each cost value by each corresponding weight value.
Question:
Sam decides he wants more jelly beans to bring home for another time. Sam places his jelly beans on the scale; it weighs 6 ounces. If everyone pays the same rate in this store, how much will his jelly beans cost? How will you calculate the cost?
Solution:
$3.60; 6 ounces multiplied by $0.60 per ounce
Question:
Is the cost proportional to the weight? How do you know?
Answer:
Yes, since the cost per ounce is the same for each, it is proportional.
Question:
What would the cost be for 0 ounces of jelly beans? Does the relationship from above hold true for 0 ounces?
Answer:
$0; yes, 0 ounces multiplied by $0.60 = $0
Example Problem and Solution
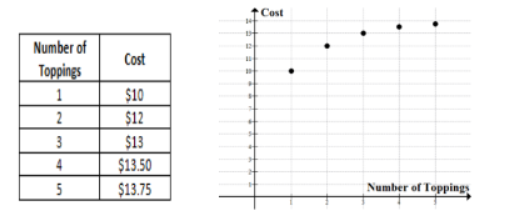
The information below represents the number of toppings on a pizza to the total cost of the pizza.
Task:
Create a table, then graph and explain if the quantities are proportional to each other or not.
The graph is not a straight line passing through the origin, so the quantities are not proportional to each other. The cost varies depending on the number of toppings.
Words to Know:
Ratio – A pair of nonnegative numbers, A: B, where both are not zero, and they are used to indicate
that there is a relationship between two quantities such that when there are A units of one quantity,
there are B units of the second quantity.
Rate – A rate indicates a proportional relationship between two quantities, how many units of one quantity there is for every 1 unit of the second quantity. For a ratio of A: B between two quantities, the rate is A/B units of the first quantity per unit of the second quantity.
Unit Rate – The numeric value of the rate, e.g., in the rate of 2.5 mph, the unit rate is 2.5.
Equivalent Ratios – Ratios that have the same value.
Topic B: Unit Rate and the Constant of Proportionality (7.RP.A.2b, 7.RP.A.2c, 7.RP.A.2d, 7.EE.B.4a)
Lessons 7-10 Video Lectures:
https://youtu.be/HdrclMzuyVA
https://www.youtube.com/watch?v=hZryTaw1lLQ
https://www.youtube.com/watch?v=QxG0nafMs9E
Constant of Proportionality
A 7th grade math tutor can help students learn to identify the constant of proportionality by finding the unit rate in a collection of equivalent ratios.
Example Problem and Answer
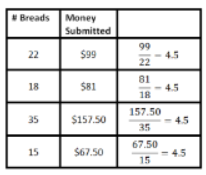
The Cougar Basketball team was raising money to attend a basketball tournament at Disney World. They decided to sell stuffed bread. James sold 22 stuffed bread and submitted $99. Michael sold 18 pieces of bread for $81. Sam sold 35 pieces of bread for $157.50. Isaac sold 15 pieces of bread for $67.50.
Create a chart to represent the number of pieces of bread sold, and the money submitted,
Solution:
The constant of proportionality is 4.5.
Question: What is the meaning of the constant of proportionality?
Answer: For each piece of bread sold, a player submitted $4.50.
Question: If Joe sold 42 pieces of bread, how much money would he submit?
Solution & Answer: Joe would submit $189.
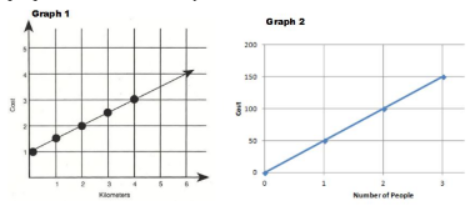
One graph is proportionate, one is not. Which is proportionate? How do you know?
Answer: Graph 2 is proportionate because it passes through the origin and contains the point (1, 50)
representing the unit rate of $50 for every person.
Example Problem and Answer
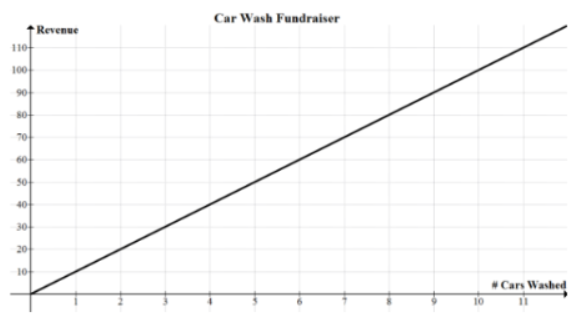
The Lady Lion softball team needed to raise money to fund travel expenses for their playoff game in Monroe. The Lady Lions conducted a car wash at the Acadiana Mall.
Below is a graph representing a portion of the revenue made from the car wash.
Task:
Write at least 4 ordered pairs from the graph and explain the meaning of each coordinate related to the scenario.
Solution:
(1, 10) means 1 car was washed for $10 of revenue
(3, 30) means 3 cars were washed for $30 of revenue
(7, 70) means 7 cars were washed for $70 of revenue
(10, 100) means 10 cars were washed for $100 of revenue
Question:
In this scenario, which is the dependent variable – number of cars washed or revenue?
Answer:
The revenue is the dependent variable because the revenue made in the fundraiser depends on the number of cars washed.
Note: The unit rate (from Topic A) is the Constant of Proportionality.
Task:
Determine the constant of proportionality and explain what it means in this scenario.
Answer:
The constant of proportionality is 10/1, which means the Lady Lions received $10 of revenue for each car washed.
Task:
Write an equation to represent the relationship.
Answer:
R = 10C; R represents Revenue; C represents # of Cars
Words to Know:
Constant of Proportionality– If a proportional relationship is described by the set of ordered pairs that satisfy the equation y = kx, where k is a positive constant, then k is called the constant of proportionality;
e.g., If the ratio of y to x is 2 to 3, then the constant of proportionality is 2/3 and y = 2/3 x.
Constant – Specifies a unique number.
Variable – A placeholder for where we might expect to see a number.
Equivalent Ratios – Ratios that have the same value.
Topic C: Ratios and Rates Involving Fractions (7.RP.A.1, 7.RP.A.3, 7.EE.B.4a)
Lessons 11-15 Video Lectures:
https://youtu.be/vIXbZjGrBEU
https://www.youtube.com/watch?v=zDy0NBnKhR4
https://www.youtube.com/watch?v=RWlWaMbdJqs
https://www.youtube.com/watch?v=S5VH_k3HROI
https://www.youtube.com/watch?v=B-e8_2O80Zs
Ratios & Rates Involving Fractions
Students will build on the knowledge of unit rates for ratios by considering application problems involving fractions. Students may need to review dividing fractions to feel more confident in these problems, and a 7th grade math tutor can help.
Example Problem and Answer
Javin would like his mother to bake cookies for his class. He would need 40 cookies for every student and teacher. Javin’s mom has a recipe that makes 10 cookies. The recipe calls for a cup of chocolate chips. If Javin’s mom has 2 cups of chocolate chips, will she have enough to make 40
cookies?
Answer:
How many does she need for 40 cookies?
Therefore, Javin’s mom does not have enough chocolate chips to make the cookies.
Equivalent Ratios
Students use tables to find an equivalent ratio of two partial quantities given a part-to-part ratio and the total of those quantities, in the third column, including problems with ratios of fractions.
Example Problem and Answer
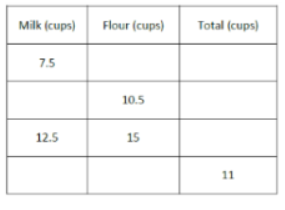
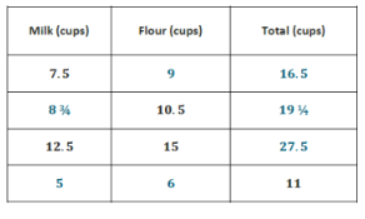
The following table shows the number of cups of milk and flour that are needed to make biscuits. Complete the table.
First, using the row that has two quantities, find the total (sum) and related ratios.
What does this mean?
The amount of milk is 56 the amount of flour.
The amount of flour is 65 the amount of milk.
Use this information to write an equation to find the missing values of the table.
For example, 65 * 7.5 = 9 cups of flour; 7.5 + 9 = 16.5 total cups
Can an equation be written to find each quantity? I so, write one for milk and one for flour.
Yes
Where M represents the amount of milk and F represents the amount of flour.
Example Problem and Answer:
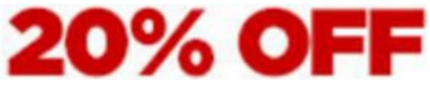
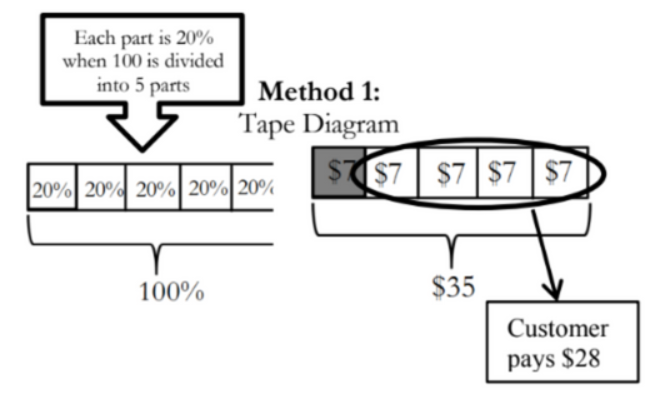
All clothing at Gennuso’s Clothing Boutique!!
Alice tried on both the $35 skirt and the $50 skirt.
Her favorite was the $35 skirt. Using the ad shown, how much will Alice actually pay for the skirt?
Topic D: Ratios of Scale Drawings (7.RP.A.2b, 7.G.A.1)
Lessons 16-22 Video Lectures:
https://www.youtube.com/watch?v=lC2bNWDzhWs
https://www.youtube.com/watch?v=92kwc__D7bI
https://www.youtube.com/watch?v=8BzHUo2VOT8
https://www.youtube.com/watch?v=5XPn_RUO6zY
Lessons 20-22: Not yet Available*
Ratios of Scale Drawings
Example Problem and Answer
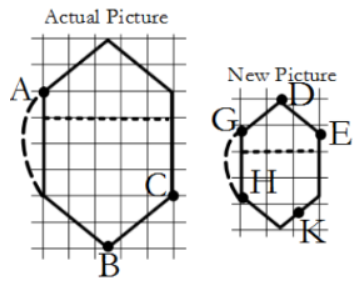
Use the following figures to answer the questions below:
Question: Is the New Picture a reduction or enlargement from the Actual Picture?
Answer: It is a reduction because the New Picture is smaller than the Actual Picture.
Question: Which point on the New Picture corresponds to point A on the Actual Picture?
Answer: Point G; Corresponding points match from one picture to another.
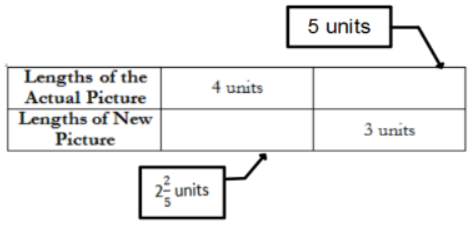
Task: Complete the chart for corresponding measurements.
Question: Does the constant of proportionality exist? If so, how do you know?
Answer: Yes, because there is a constant value 53 to get from each length to its corresponding length. (See work and values below).
Students learn the term scale factor and recognize the constant of proportionality. With the scale factor, students make scale drawings of pictures and diagrams.
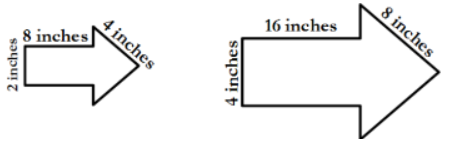
Question:
Given the figures below, find the scale factor.
The scale factor is 2. Create a ratio of corresponding lengths of the scale drawing to the original drawing.
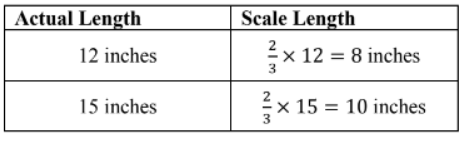
Question:
Reverse the process. If given the dimensions of the original drawing, compute the dimensions of the scale drawing if the scale factor is
Steps to check for proportionality for the scale drawing and original object/picture:
1) Measure lengths of the scale drawing. Record on the table.
2) Measure corresponding lengths on the actual
picture/drawing. Record on the table.
3) Check for the constant of proportionality.
Words to Know:
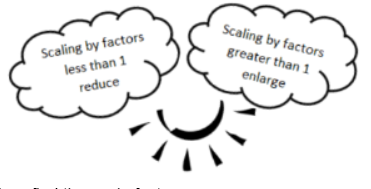
Scale Drawing – a reduced or enlarged two-dimensional drawing of an original two-dimensional drawing.
One-to-One Correspondence – Each point in one figure corresponds to one and only one point in the second figure.
Scale Drawing – A drawing in which all lengths between points or figures in the drawing are reduced or enlarged proportionally to the lengths in the actual picture. A constant of proportionality exists between the corresponding lengths of the two images.
Reduction – The lengths in the scale drawing are smaller than those in the actual object or picture.
Enlargement/Magnification: The lengths in the scale drawing are larger than those in the actual object or picture.
Scale Factor: corresponds to the unit rate and the constant of proportionality. It can be calculated from
the ratio of any length in the scale drawing to its corresponding length in the actual picture.
*The following information was obtained from Embarc.Online (a website that was originally created to support local teachers using Eureka Math, but we now serve 30,000 users each day across the nation). This information is applicable to all math users.
Reference: (n.d.). Grade 7 Module 1. Embarc.Online. https://embarc.online/course/view.php?id=61
TESTIMONIALS
Ethan was very happy with the sessions and I could see his increased confidence in Math classes at school. Ethan’s grades were generally improved in his IB maths assessments and his MAP percentile ranking increased from 78 to 87%. During this time, Ethan missed 2 of his 5 school Math classes each week for tennis training. Sam provided the math support we needed at home to cover the curriculum but also worked well to fill gaps in his knowledge from previous years.
-Caroline B.
This company is great in finding awesome learning specialists who work with kids of all ages and use multisensory techniques to help break down abstract concepts. My child needs help with math and they were able to supply my child with a top-notch math tutor who was able to really help my son improve. Not only is it hard to find qualified math learning specialists who work well with school aged children, but they come to your home, which is a real godsend.
-Mr. K. Kim
I want to thank you for the wonderful math tutoring you did with V! We really can see the changes in her self-confidence. It has been encouraging to see her improving her math grades. She is a big fan of yours, as are we. Because of the way LaGuardia HS is structuring classes for the year, V’s math class has now ended. Regardless, we will want Gillian to tutor V again when math officially starts up again in the fall.
-J.G.
My child worked with Gillian D virtually for math enrichment. She is an excellent teacher. She took time to understand my child’s specific learning style and provided tools that would be engaging. She was kind and empathetic- really made it her goal to connect with my child and build trust and rapport. My child started the school year with confidence and without the typically “brain-drain” that occurs over the summer, thanks to Gillian.
-Nicole May
Chris has been wonderful working with U on math for the past few months, she adores him!
-Z.K.
MEET OUR MATH TUTORS WHO COULD COME TO YOUR HOME

CAILIN
M.A. – Special Education

MELISSA
Certified Math and Special Education Teacher, MS Math Education

AARON

LEAH
Bachelor’s degree in Secondary Education with a Concentration in Mathematics, M.S. in General and Special Education (grades 1-6)

JEFFREY
Master’s in Mathematics Education(5-9)

TRACY
Certified Special Education Teacher

EVAN
Master’s in Leadership in Math Education, Bachelor’s Degree in Mathematics

KARINA
LEARN MORE ABOUT MATH TUTORING SERVICES:
⏩ Long Island Math Tutoring
⏩ Upper East Side Math Tutoring
⏩ North and Central NJ Math Tutoring
⏩ Long Island Middle and High School Math Tutoring
⏩ Hudson, County NJ Middle and High School Math Tutoring
⏩ Manhattan Middle and High School Math Tutoring
⏩ Bronx Middle and High School Math Tutoring
⏩Manhattan In-home Math Tutoring
⏩ Best Brooklyn Math Tutors
⏩ Remote IB Math Tutoring
Chat with Themba Tutors Today! Our 7th Grade Math Tutors are ready to help you right now!
FREE CONSULTATION WITH A NYC TUTOR!!!
Call: (917) 382-8641, Text: (833) 565-2370
Email: [email protected]
(we respond to email right away!).
Craig Selinger
Latest posts by Craig Selinger (see all)
- Psychotherapy and Support Services at Cope With School NYC - April 12, 2024
- NYC Parents of Teens Support Group - April 8, 2024
- Here I Am, I Am Me: An Illustrated Guide to Mental Health - April 4, 2024






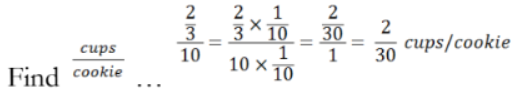
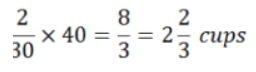

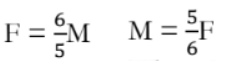

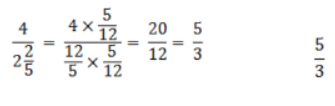
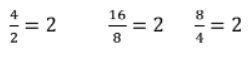
No Comments