
07 Jan Manhattan Algebra 2 Tutor
MANHATTAN ALGEBRA 2 TUTOR

WE travel to YOUR NYC home:
WE also travel to:
Module 1: Polynomial, Rational, and Radical Relationships
A: Introduction to Polynomials
A polynomial is an expression composed of variables, constants, and exponents that are combined using mathematical operations such as addition, subtraction, multiplication, and division (No division operation by a variable).
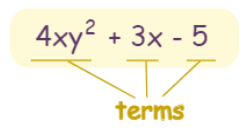
A polynomial looks like this:
an example of a polynomial with 3 terms
Polynomials with one variable make nice smooth curves:

constants (like 3, −20, or ½)
variables (like x and y)
exponents (like the 2 in y2), but only 0, 1, 2, 3, … etc are allowed
that can be combined using addition, subtraction, multiplication, and division.
A polynomial can have constants, variables, and exponents, but never division by a variable. Also, they can have one or more terms but not an infinite number of terms.
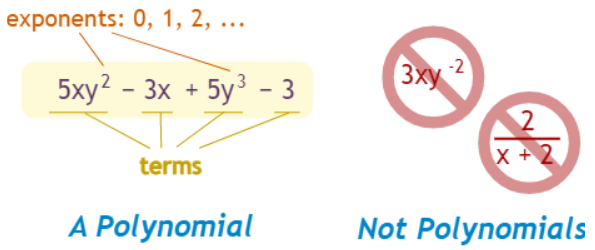
Polynomial or Not?
These are polynomials:
3x
x − 2
−6y2 − (7/9)x
3xyz + 3xy2z − 0.1xz − 200y + 0.5
512v5 + 99w5
5
(Yes, “5” is a polynomial, one term is allowed, and it can be just a constant!)
These are not polynomials
3xy-2 is not, because the exponent is “-2” (exponents can only be 0,1,2,…)
2/(x+2) is not, because dividing by a variable is not allowed
1/x is not either
√x is not, because the exponent is “½” (see fractional exponents)
But these are allowed:
x/2 is allowed, because you can divide by a constant
also 3x/8 for the same reason
√2 is allowed, because it is a constant (= 1.4142…etc)
Monomial, Binomial, Trinomial
There are special names for polynomials with 1, 2 or 3 terms:
How do you remember the names? Think cycles!
There is also quadrinomial (4 terms) and quintinomial (5 terms), but those names are not often used.
Variables
Polynomials can have no variable at all.
Example: 21 is a polynomial. It has just one term, which is a constant.
They may have one variable
Example: x4 − 2×2 + x has three terms, but only one variable (x)
Or two or more variables
Example: xy4 − 5x2z has two terms, and three variables (x, y and z)
What is Special About Polynomials?
Because of the strict definition, polynomials are easy to work with.
For example, we know that:
If you add polynomials you get a polynomial
If you multiply polynomials you get a polynomial
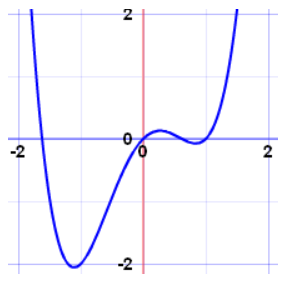
So you can do lots of additions and multiplications, and still have a polynomial as the result. Also, polynomials of one variable are easy to graph, as they have smooth and continuous lines.
Example: x4−2×2+x
See how nice and smooth the curve is?
You can also divide polynomials (but the result may not be a polynomial).
Degree
The degree of a polynomial with only one variable is the largest exponent of that variable.
Example:
4×3 − x + 2
The Degree is 3 (the largest exponent of x)
Standard Form
The Standard Form for writing a polynomial is to put the terms with the highest degree first.
Example: Put this in Standard Form: 3×2 − 7 + 4×3 + x6
The highest degree is 6, so that goes first, then 3, 2, and then the constant last:
x6 + 4×3 + 3×2 − 7
Common Symbols Used in Algebra
Symbol
+
−
×
·
/
√
( )
[ ]
{ }
=
≈
≠
< ≤
> ≥
⇒
⇔
∴
!
Meaning
add
subtract
multiply
multiply (as “×” can look like “x”)
divide
square root (“radical”)
cube root
nth root
grouping symbols (round brackets)
grouping symbols (square brackets)
set symbols (curly brackets)
equals
approximately equal to
not equal to
less than, less than or equal to
greater than, greater than or equal to
implies (if … then)
“if and only if” or iff or “is equivalent to”
Therefore
Factorial
Example
3+7 = 10
5−2 = 3
4×3 = 12
4·3 = 12
20/5 = 4
√4 = 2
∛8 = 2
2(a−3)
2[ a−3(b+c) ]
{1,2,3}
1+1 = 2
π ≈ 3.14
π ≠ 2
2 < 3
5 > 1
a and b are odd ⇒ a+b is even
x=y+1 ⇔ y=x−1
a=b ∴ b=a
4! = 4×3×2×1 = 24
Topic B: Adding and Subtracting Polynomials
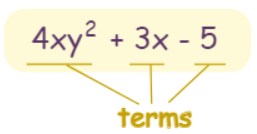
A polynomial looks like this:
example of a polynomial
this one has 3 terms
To add polynomials we simply add any like terms together. Like Terms are terms whose variables (and their exponents, such as the 2 in x2) are the same.
In other words, terms that are “like” each other.
Note: the coefficients (the numbers you multiply by, such as “5” in 5x) can be different.
Example:
7x x -2x πx
are all like terms because the variables are all x
Example:
(1/3)xy2 -2xy2 6xy2 xy2/2
are all like terms because the variables are all xy2
Example: These are NOT like terms because the variables and/or their exponents are different:
2x 2x2 2y 2xy
Adding Polynomials
Step 1: Arrange each polynomial with the term with the highest degree first then in decreasing order of degree.
Step 2: Group the like terms. Like terms are terms whose variables and exponents are the same.
Step 3: Simplify by combining like terms.
Example: Add 2×2 + 6x + 5 and 3×2 – 2x – 1
Start with:
2×2 + 6x + 5 + 3×2 − 2x − 1
Place like terms together:
2×2+3×2 + 6x−2x + 5−1
Which is:
(2+3)x2 + (6−2)x + (5−1)
Add the like terms:
5×2 + 4x + 4
Other Examples:
(adding in columns)
Adding Several Polynomials – Using columns helps us to match the correct terms together in a complicated sum.
Example: Add (2×2 + 6y + 3xy) , (3×2 – 5xy – x) and (6xy + 5)
Line them up in columns and add:
2×2 + 6y + 3xy
3×2 – 5xy – x
6xy + 5
5×2 + 6y + 4xy – x + 5
Subtracting Polynomials
To subtract Polynomials, first reverse the sign of each term we are subtracting (in other words turn “+” into “-” and “-” into “+”), then add as usual.
Note: After subtracting 2xy from 2xy we ended up with 0, so there is no need to mention the “xy” term anymore.
Topic C: Multiplying Polynomials
To be able to multiply polynomials,
First, multiply each term in one polynomial by each term in the other polynomial using the distributive law.
Add the powers of the same variables using the exponent rule.
Then, simplify the resulting polynomial by adding or subtracting the like terms.
example of a polynomial
this one has 3 terms
1 term × 1 term (monomial times monomial)
To multiply one term by another term, first multiply the constants, then multiply each variable together and combine the result, like this (press play):
(Note: I used “·” to mean multiply. In Algebra we don’t like to use “×” because it looks too much like the letter “x”)
1 term × 2 terms (monomial times binomial)
Multiply the single term by each of the two terms, like this:
2 term × 1 terms (binomial times monomial)
Multiply each of the two terms by the single term, like this:
(I did that one a bit faster by multiplying in my head before writing it down)
2 terms × 2 terms (binomial times binomial)
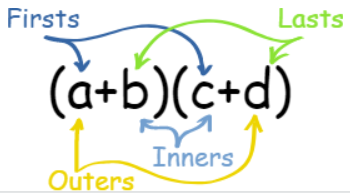
We can multiply them in any order so long as each of the first two terms gets multiplied by each of the second two terms. But there is a handy way to help us remember to multiply each term called “FOIL”.
It stands for “Firsts, Outers, Inners, Lasts”:
Firsts: ac
Outers: ad
Inners: bc
Lasts: bd
So you multiply the “Firsts” (the first terms of both polynomials), then the “Outers”, etc. Let us try this on a more complicated example:
2 terms × 3 terms (binomial times trinomial)
“FOIL” won’t work here, because there are more terms now. But just remember: Multiply each term in the first polynomial by each term in the second polynomial
Like Terms
And always remember to add Like Terms:
Example: (x + 2y)(3x − 4y + 5)
(x + 2y)(3x − 4y + 5)
= 3×2 − 4xy + 5x + 6xy − 8y2 + 10y
= 3×2 + 2xy + 5x − 8y2 + 10y
Note: −4xy and 6xy are added because they are Like Terms.
Also note: 6yx means the same thing as 6xy
Long Method
Choose one polynomial (the longest is a good choice) and then:
- multiply it by the first term of the other polynomial, writing the result down
- then multiply it by the second term of the other polynomial, writing the result under the matching terms from the first multiplication
- then multiply it by the third term of the other polynomial (if any), etc.
- lastly, add up the columns.
By lining up the columns and being careful to put the terms under the correct columns, the job becomes “automatic”, and we can easily look back to see if we got it right, too.
But what happens if a polynomial is missing, say, an x term or an x2 term? Just leave that column blank!
Here is a more complicated example with blank gaps:
More than One Variable
So far, we have been multiplying polynomials with only one variable (x), but how do we handle polynomials with two or more variables (such as x and y)? What are the column headings?
Just ignore the columns in the question, and write down the answers as they come, always checking to see if we could put an answer under a matching answer:
Topic D: Dividing Polynomials
Sometimes it is easy to divide a polynomial by splitting it at the “+” and “−” signs, like this (press play):
When the polynomial was split into two parts we still had to keep the “/3” under each one.
Then the highlighted parts were “reduced” (6/3 = 2 and 3/3 = 1) to leave the answer of 2x-1
Here is another, slightly more complicated, example:
What happened?
- The 1st Term had x2 above and x below, which together becomes just x
- The 2nd Term had x above and below, so they canceled each other out
- We couldn’t simplify “1/3x” any further.
That is as far as we can get. But the answer is still “simpler”
Note: the result is a valid answer but is not a polynomial, because the last term (1/3x) has division by a variable (x).
Now, sometimes it helps to rearrange the top polynomial before dividing, as in this example:
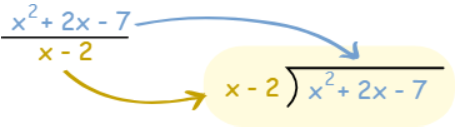
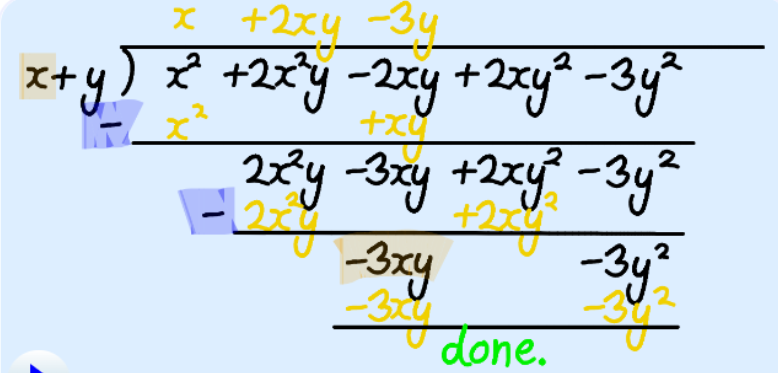
Long Division
Dividing the Numerator by the Denominator
We can give each polynomial a name:
- the top polynomial is the numerator
- the bottom polynomial is the denominator
If you have trouble remembering, think denominator is down-nominator.
Write it down neatly:
- the denominator goes first,
- then a “)”,
- then the numerator with a line above
Both polynomials should have the “higher order” terms first (those with the largest exponents, like the “2” in x2).
Then:
- Divide the first term of the numerator by the first term of the denominator and put that in the answer.
- Multiply the denominator by that answer, put that below the numerator
- Subtract to create a new polynomial
- Repeat, using the new polynomial It is easier to show with an example!
Example:
Write it down neatly like below, then solve it step-by-step:
Check the answer:
Multiply the answer by the bottom polynomial, and we should get the top polynomial:
Remainders
The previous example worked perfectly, but that is not always so! Try this one:
After dividing we were left with “2”, this is the “remainder”.
The remainder is what is left over after dividing.
But we still have an answer: put the remainder divided by the bottom polynomial as part of the answer, like this:
“Missing” Terms
There can be “missing terms” (example: there may be an x3, but no x2). In that case either leave gaps or include the missing terms with a coefficient of zero.
Example:
Write it down with “0” coefficients for the missing terms, then solve it normally:
More than One Variable
So far, we have been dividing polynomials with only one variable (x), but we can handle polynomials with two or more variables (such as x and y) using the same method.
Example:
Solution:
Students of all ages receive one-on-one guidance in all instructional materials, exam preparation, and executive function therapy. At Themba Tutors, we take the time to help students and clients appreciate their strengths and succeed in areas where they need to improve. We offer personalized tools for each of our clients to help them become more aware of their individual needs as they work toward short-term goals. These skills will assist our students/clients in achieving their long-term goals.
TESTIMONIALS
Jordan tutored our son in 7th grade math. We had a wonderful experience with Jordan. He was knowledgeable, always on time, and came up with some good strategies for our son to tackle difficult math concepts. Our son has a nonverbal learning disability so working with him can be somewhat challenging at times. But Jordan was always up to the task!
-ANNE S.
Ethan was very happy with the sessions and I could see his increased confidence in math classes at school. Ethan’s grades were generally improved in his IB math assessments and his MAP percentile ranking increased from 78 to 87%. During this time, Ethan missed 2 of his 5 school Math classes each week for tennis training. Sam provided the math support we needed at home to cover the curriculum but also worked well to fill gaps in his knowledge from previous years.
-CAROLINE
My son, a junior in a private high school worked, with a wonderful tutor from Themba to get ready for his SATs. I spoke with Blythe and she asked detailed questions about my sons strengths and weaknesses. She put me in touch with Don, who worked beautifully with my son. Don immediately understood where my son needed help and focused their time together on specific areas of need. He also recognized my sons strengths ( math )and was able to accelerate his understanding in those areas. My sons score jumped 190 points! The individualized instruction he got from Themba and Don was amazing! I highly recommend these wonderful people.
-MARIE W.
My daughter, a freshman in a public high school, was struggling in math. I got in touch with Blythe at Themba, and she managed to have a wonderful math tutor come to my home the following day. She stayed much more than the required time to make sure that my daughter understood all the concepts. She also followed up with us and asked if we had any other questions that she could help with. As a parent, it is a relief to know that you can secure a tutor very quickly who comes straight to your home.
A great experience!
-TIPHAINE M
My experience with Themba Tutors was awesome. When I was introduced to the service I told them my needs and based on that they set me up with a range of tutors to choose from. I chose to work with Paul who was the best tutor that I have ever worked with. I was studying for the New Jersey state teacher exam there was a number of subject areas that I had to study and one of them was math. Paul helped me understand the math on the test. He explained it to me in away that made it easy and he gave me tools to practice on my own. In addition to helping me with math skills he gave wonderful study tips and tricks to use to help me study the material that I had to learn. Paul was a pleasure to work with and O thank him for helping me pass the test
-ESTHER B
MEET OUR MANHATTAN ALGEBRA 2 TUTORS WHO TRAVELS TO YOUR HOME:

JOHN
Master’s in STEM Education and Master’s in Applied Math

KRISTEN
Master’s degree in Actuarial Science

SAMARA
Master’s Degree in Adolescent Special Education

EVAN
Master’s in Leadership in Math Education, Bachelor’s Degree in Mathematics

TRACY
Certified Special Education Teacher

LEAH
Bachelor’s degree in Secondary Education with a Concentration in Mathematics, M.S. in General and Special Education (grades 1-6)

MELISSA
Certified Math and Special Education Teacher, MS Math Education
**Guarantee: It’s critical that whoever receives our tutoring services connects with the specialist, the specialist has expertise in the area of need, and is available to travel to you. If you are not 100% satisfied with our services, we are 100% committed to finding you the right professional.
Chat with Themba Tutors Today! Our Manhattan Algebra 2 Tutors are ready to help you right now!
FREE CONSULTATION!!!
Call: (917) 382-8641, Text: (833) 565-2370
Email: [email protected]
(we respond to email right away!).
References:
https://www.mathsisfun.com/algebra/index-2.html
Craig Selinger
Latest posts by Craig Selinger (see all)
- Psychotherapy and Support Services at Cope With School NYC - April 12, 2024
- NYC Parents of Teens Support Group - April 8, 2024
- Here I Am, I Am Me: An Illustrated Guide to Mental Health - April 4, 2024






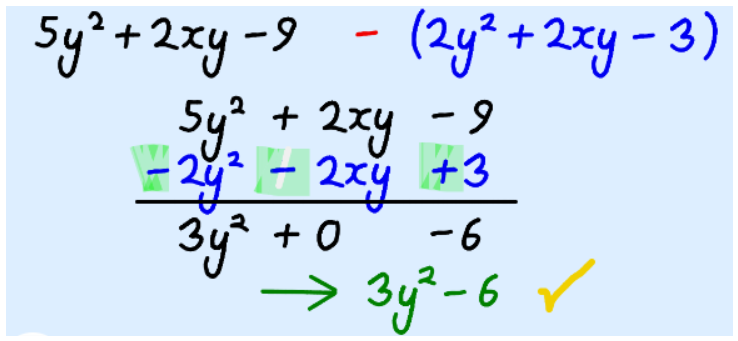
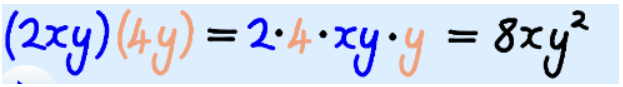
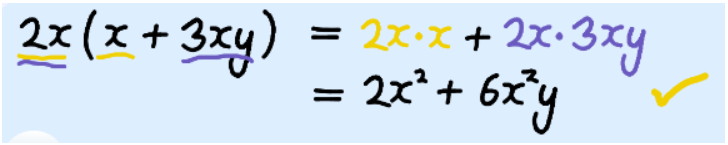
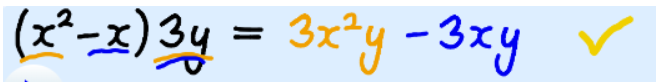
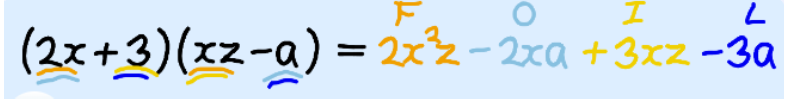
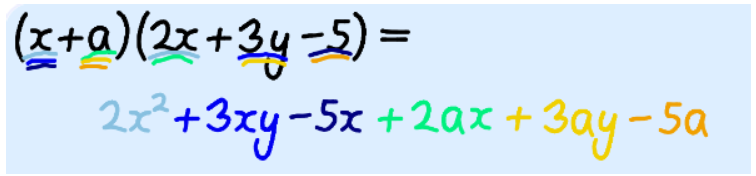


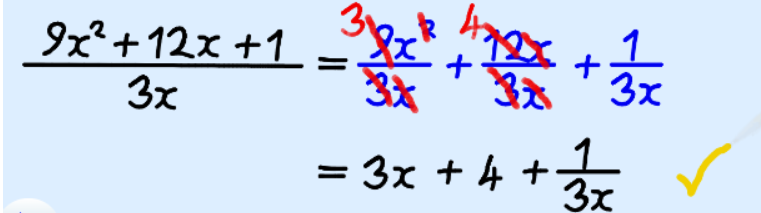


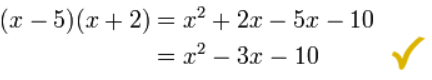
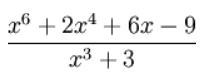
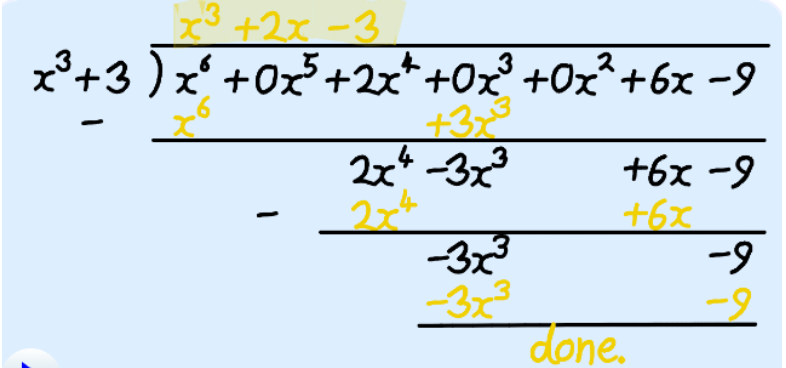
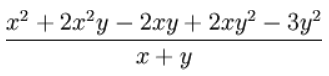

No Comments