05 Jan Manhattan Algebra 1 Tutor
Cornerstone Protection
836 Euclid Avenue Suite 16, Lexington
-
Amazing assistance provided by Shannon today on my security system. I’m so grateful for your prompt, efficient, professional, and courteous service. Put me down as a customer for life!
-
One of the most painless experiences I've had. They came on time and was over the moon professional with still keeping a level of personability to it. The gentleman also went out of his way to say that my husband and Mines business … More was appreciated. Which is actually rare to be appreciated by such a great company. So thank you and we look forward to continuing services with this company.
-
I am so happy we decided to go with cornerstone. They were quick and efficient. Shannon and the installer we very friendly. We got a lot of equipment and it was still within our budget. 10/10 would definitely recommend! Thank you
-
Love the customer service and Shanon and his team go above and beyond for my restaurant. Couldn't of asked for a better security system and level of service that his team provides.
-
I have been using Cornerstone Protection service for over 5 years and I'm really happy with the service and state-of-the-art equipments and it's futures are so much in advance and friendly, I highly recommend Cornerstone Protection … More Service any and all business that need a security protection days and nights specially after business hours(Cornerstone Protection is perfect solution for your business). Owner of Cornerstone Protection is proactive with their customers and their equipments. Good experienced with Cornerstone Protection!!!
Kanu Patel -
We had a very positive experience with Alissa as a tutor for our pod of 5th grade boys from January - June 2020. She cared a lot about the boys and worked hard to create meaningful activities for them. The pod experience was invaluable … More for all of our families during a difficult year and we were so grateful to have found this partnership! We also want to appreciate Craig for helping to match us with a tutor on very short notice after we had cycled through a few folks who were not able to see the commitment through. Thanks for sticking with us!
-
Dusty was the exact person we needed to help our child finish out the school year. So grateful to him for the way he steadily encouraged her and helped her stay on track and organized. He is flexible, responsive to our needs/schedule as … More a family, and a delight to be with. We are also thankful that Craig at Themba Tutors really "gets it" and partnered us with such a wonderful tutor who was a great fit for our girl.
-
My child worked with Gillian D virtually for math enrichment. She is an excellent teacher. She took time to understand my child's specific learning style and provided tools that would be engaging. She was kind and empathetic- really … More made it her goal to connect with my child and build trust and rapport. My child started the school year with confidence and without the typically "brain-drain" that occurs over the summer, thanks to Gillian.
-
I am going into my second year as a Themba tutor. I have met so many great individuals while working for this company. Craig and the rest of the Themba team do such an excellent job picking and choosing Themba tutors that suit each client's … More individual needs! I look forward to meeting new tutors and clients in the 2021-2022 school year!
-
Our son started in a new high school, 100% remote, and was really struggling with Latin and Physics. I found Themba Tudors online and had an initial call with Craig, who was very knowledgeable, responsive, and found 2 amazing tutors for … More us. Both the Latin and the physics tutors were fantastic, connected with my son really well and helped him go from 'failing' grade to 'honors'! I will for sure continue using (and recommending!) Themba Tutors. Thank you, C, K, and W!
-
Brian is a fantastic executive functioning coach. Super helpful, flexible with hours, and tailored the experience to our needs.
-
Giulia Mercuri is a great Italian tutor! She was very responsive and accessible. Giulia put a ton of effort into preparing for each session and really helped our son with test preparation and projects. We are grateful that she was able … More to help, especially since our son did not receive any live teaching during COVID. We are happy that she was referred to us! -
As an adult student diagnosed with a learning disability during grad school, I knew I needed help dealing with my Master's program's demanding workload. I was seriously considering dropping out when I was referred to Themba Tutors. … More I was paired up with a wonderful tutor, Julie, who was a total lifesaver. I learned many techniques that I can utilize in the future as I embark on the next phase of my career.
I can wholeheartedly say after working with Themba for two years that I would not have finished my program without this organization. And I am so thankful I selected them. -
We were introduced to a wonderful tutor: Mcedwyn. He and our son, a freshman in college, worked well together. As a result, our son’s grades significantly improved. The tutor taught our son subject content and various methods to effectively … More study for quizzes and exams. Our son was also taught time management and organization. My son’s experience with the tutor made the first year of college a less intimidating experience. -
We have been with our tutor, Cailin Schiller, for two years, from 5th - 7th grade. She started as an executive functioning tutor with my daughter. From the start, she demonstrated a depth of expertise and a selective use of techniques skillfully … More adapted to my daughter’s ADHD and Math disability. Cailin made Math accessible and understandable to her in a way that even her teachers had not been able to do. She differentiated reading, writing and math tasks and assignments to tailor them to my daughter’s unique learning differences. Not only did it have an effect on her grades and her work efficiency, but she finally could do her work with less anxiety. Even my daughter’s teachers used Cailin’s guidance to modify their work with her. But most importantly, she became my daughter’s favorite resource. I can’t say how invaluable Cailin has been to my daughter’s progress and well-being. I’d recommend her a million times over. She is a gem. -
Victoria is a superb tutor. She helped my high school age daughter with her writing. Victoria's skills as a tutor, as well as her sense of humor and her engaging personality went a long way with my daughter. -
Themba Tutors provided a leaning specialist that was a perfect fit for my daughter. I told them what we were looking for and they delivered. Our tutor is responsive and flexible and makes it easy for my daughter to reach out to her own … More her own, which gives her an added sense of responsibility over her learning. As a therapist myself, I now regularly recommend Themba to my patients. A much needed and well provided service to the community!! -
The tutors at Themba are fantastic! Caitlyn McNeill helped our son academically, but also with getting organized in every subject, which he so desperately needed. She offered great advice and useful strategies that helped our son become … More a more successful student. We are using Themba tutors again this year for our daughter. We're so happy to have been referred to them! -
I'm so glad we were referred to Themba Tutors. After a great initial conversation to learn our needs, we were connected with an excellent tutor, Felicia, who is helping our high school daughter learn better organizational and executive … More skills. Highly recommended. -
We had a wonderful experience with our tutor Micaela. She helped our son not only academically but at every level. We will be forever grateful to have her in our lives. -
The tutors at Themba are fantastic! Caitlyn McNeill helped our son academically, but also with getting organized in every subject, which he so desperately needed. She offered great advice and useful strategies that helped our son become … More a more successful student. We are using Themba tutors again this year for our daughter. We're so happy to have been referred to them!
-
Paul Smith at Themba has been an exceptional tutor for my son, both in terms of teaching the subject matter and teaching how best to approach the process of learning math and executing assignments. We feel very fortunate to be working with … More Paul. -
We were very lucky to have found Edwouine Swift, my son's therapist through Themba Tutors. Thomas is 12 years old, and it is extremely difficult to get him to write. Edwouine just works her magic with him, he adores her and is so … More eager to follow her guidance. I have no doubt she will be a positive driving force in his academic future.
MANHATTAN ALGEBRA 1 TUTOR
WE travel to YOUR NYC home:
WE also travel to:
Manhattan Algebra 1 Tutoring
Module 1: Numbers
Topic A: Squares and Square Roots
Lesson Objective: Perform the four arithmetic operations using radical terms that are the same and different and write the result in its simplest form.
Squares
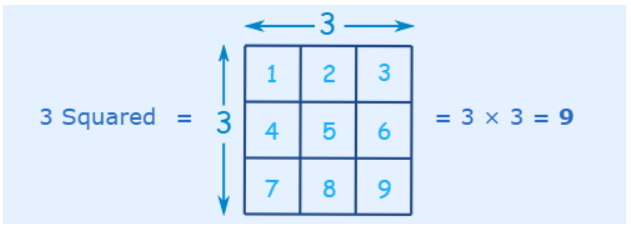
To square a number, just multiply it by itself.
Example: What is 3 squared?
“Squared” is often written as a little 2 like this:
This says “4 Squared equals 16”
(the little 2 means the number appears twice in multiplying, so 4×4=16)
Square Root
A square root goes the other direction:
3 squared is 9, so a square root of 9 is 3 
A square root of x is a number r whose square is x:
r is a square root of x
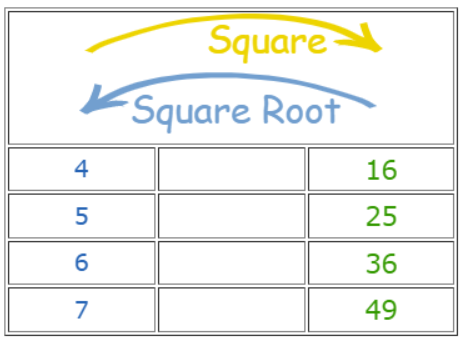
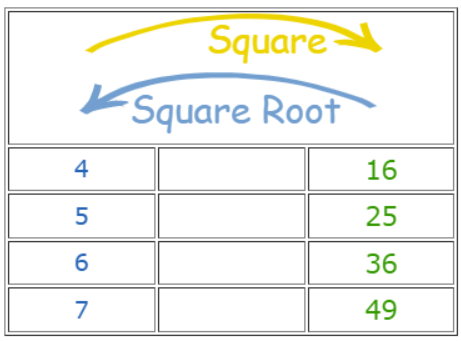
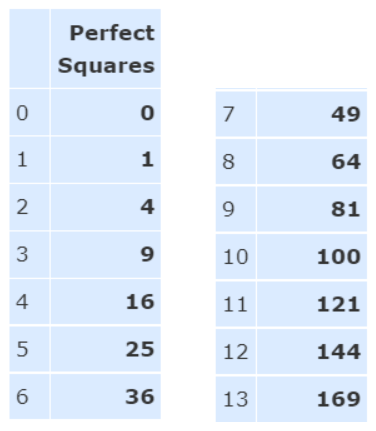
Here are some more squares and square roots:
Negatives
We discovered earlier that we could square negative numbers:
Example: (−3) squared
(−3) × (−3) = 9
And, of course 3 × 3 = 9 also.
So the square root of 9 could be −3 or +3
Example: What are the square roots of 25?
(−5) × (−5) = 25
5 × 5 = 25
So the square roots of 25 are −5 and +5
The Square Root Symbol
This is the special symbol that means “square root” it is sort of like a tick and actually started hundreds of years ago as a dot with a flick upwards. It is called the radical and always makes mathematics look important!
and we say, “square root of 9 equals 3”
Example: What is √25?
25 = 5 × 5, in other words when we multiply 5 by itself (5 × 5) we get 25
So the answer is: √25 = 5
But wait a minute! Can’t the square root also be −5? Because (−5) × (−5) = 25 too.
Well the square root of 25 could be −5 or +5.
But when we use the radical symbol √ we only give the positive (or zero) result.
Example: What is √36?
Answer: 6 × 6 = 36, so √36 = 6
Perfect Squares
The Perfect Squares (also called “Square Numbers”) are the squares of the integers.
Calculating Square Roots
It is easy to work out the square root of a perfect square, but it is really hard to work out other square roots.
Example: what is √10?
Well, 3 × 3 = 9 and 4 × 4 = 16, so we can guess the answer is between 3 and 4.
Let’s try 3.5: 3.5 × 3.5 = 12.25
Let’s try 3.2: 3.2 × 3.2 = 10.24
Let’s try 3.1: 3.1 × 3.1 = 9.61
…
Getting closer to 10, but it will take a long time to get a good answer!
At this point, I get out my calculator and it says:
3.1622776601683793319988935444327
But the digits just go on and on, without any pattern.
So even the calculator’s answer is only an approximation
Note: numbers like that are called Irrational Numbers if you want to know more.
A Fun Way to Calculate a Square Root
There is a fun method for calculating a square root that gets more and more accurate each time around:
a) start with a guess (let’s guess 4 is the square root of 10) around
b) divide by the guess (10/4 = 2.5)
c) add that to the guess (4 + 2.5 = 6.5)
d) then divide that result by 2, in other words, halve it. (6.5/2 = 3.25)
e) now, set that as the new guess, and start at b) again
And so, after 3 times around the answer is 3.1623, which is pretty good, because:
3.1623 x 3.1623 = 10.00014
Now … why don’t you try calculating the square root of 2 this way?
How to Guess
What if we have to guess the square root for a difficult number such as “82,163” … ? In that case we could think “82,163” has 5 digits, so the square root might have 3 digits (100×100=10,000), and the square root of 8 (the first digit) is about 3 (3×3=9), so 300 is a good start.
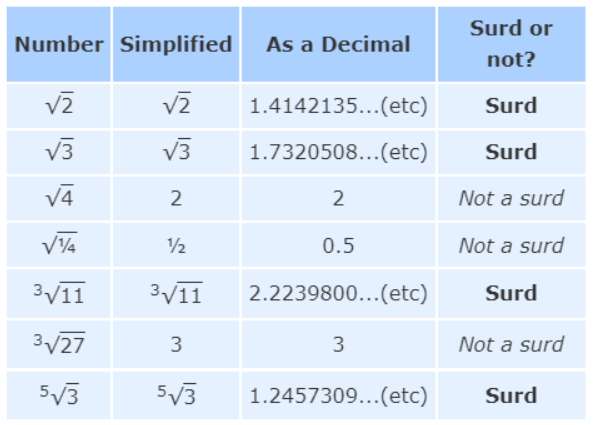
Surds
When we can’t simplify a number to remove a square root (or cube root etc.,) then it is a surd.
Example: √2 (square root of 2) can’t be simplified further so it is a surd
Example: √4 (square root of 4) can be simplified (to 2), so it is not a surd!
Have a look at some more examples:
The surds have a decimal that goes on forever without repeating, and are Irrational Numbers.
Simplifying Square Roots
To simplify a square root: make the number inside the square root as small as possible (but still a whole number):
Example: √12 is simpler as 2√3
Get your calculator and check if you want: they are both the same value!
Here is the rule: when a and b are not negative
√(ab) = √a × √b
Example: simplify √12
12 is 4 times 3: √12 = √(4 × 3)
Use the rule: √(4 × 3) = √4 × √3
And the square root of 4 is 2: √4 × √3 = 2√3
So √12 is simpler as 2√3
Example: simplify √8
√8 = √(4×2) = √4 × √2 = 2√2
(Because the square root of 4 is 2)
Example: simplify √18
√18 = √(9 × 2) = √9 × √2 = 3√2
*It often helps to factor the numbers (into prime numbers is best):
Example: simplify √6 × √15
First we can combine the two numbers:
√6 × √15 = √(6 × 15)
Then we factor them:
√(6 × 15) = √(2 × 3 × 3 × 5)
Then we see two 3s, and decide to “pull them out”:
√(2 × 3 × 3 × 5) = √(3 × 3) × √(2 × 5) = 3√10
Fractions
There is a similar rule for fractions:
Example: simplify √30 / √10
First we can combine the two numbers:
√30 / √10 = √(30 / 10)
Then simplify:
√(30 / 10) = √3
Example: simplify
√20 × √5
√2
See if you can follow the steps:
√20 × √5
√2
√(2 × 2 × 5) × √5
√2
√2 × √2 × √5 × √5
√2
√2 × √5 × √5
√2 × 5
5√2
Example: simplify 2√12 + 9√3
First simplify 2√12:
2√12 = 2 × 2√3 = 4√3
Now both terms have √3, we can add them:
4√3 + 9√3 = (4+9)√3 = 13√3
Principal Square Root
So if there are really two square roots, why do people say √25 = 5 ? Because √ means the principal square root … the one that isn’t negative! There are two square roots, but the symbol √ means just the principal square root.
Example:
The square roots of 36 are 6 and −6
But √36 = 6 (not −6)
The Principal Square Root is sometimes called the Positive Square Root (but it can be zero).
Plus-Minus Sign
± is a special symbol that means “plus or minus”,
so instead of writing:
w = √a and w = −√a
we can write:
w = ±√a
In a Nutshell, When we have: r2 = x, then: r = ±√x
Reference:
Students of all ages receive one-on-one guidance in all instructional materials, exam preparation, and executive function therapy. At Themba Tutors, we take the time to help students and clients appreciate their strengths and succeed in areas where they need to improve. We offer personalized tools for each of our clients to help them become more aware of their individual needs as they work toward short-term goals. These skills will assist our students/clients in achieving their long-term goals.
MEET OUR MANHATTAN ALGEBRA 1 TUTORS WHO TRAVELS TO YOUR HOME:
DAN
M.S. Ed., NYS Certified Childhood General and Special Education (Grades 1-6)
MICHELLE L.
Bachelor of Science degree in Cognitive Science with minors in psychology and disabilities studies, Masters in Speech and Language Pathology, & Juris Doctor degree from New York Law School
NICOLE
Elementary School Teacher, Master’s in Special Education and General Education (1-6)
KIRSTEN
M.S. Ed., NYS Certified Childhood General and Special Education (Grades 1-6)
ELIZABETH
Bachelor’s degree in Childhood Education & Students with Disabilities (Grades 1-6), Master’s degree in Childhood Education & Students with Disabilities (Grades 1-6)
**Guarantee: It’s critical that whoever receives our tutoring services connects with the specialist, the specialist has expertise in the area of need, and is available to travel to you. If you are not 100% satisfied with our services, we are 100% committed to finding you the right professional.
Chat with Themba Tutors Today! Our Manhattan Algebra 1 Tutors are ready to help you right now!
FREE CONSULTATION!!!
Call: (917) 382-8641, Text: (833) 565-2370
Email: [email protected]
(we respond to email right away!).
Craig Selinger
Latest posts by Craig Selinger (see all)
- The Value of Expert ADHD Coaching in Unlocking School Success - June 9, 2023
- The Benefits of Hiring a Coach for ADHD Management - June 8, 2023
- Transition Strategies for Students with ADHD - June 7, 2023
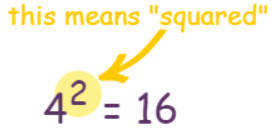
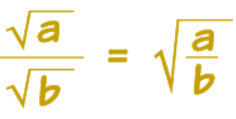
No Comments